七年级动角问题：寻找旋转中的数量关系

动态几何图形的数量关系，对于七年级学生来讲，稍有难度，刚刚从小学经过一学期的适应，几何刚刚入门，所涉及到知识点很少，角的计算，角平分线等。纯粹从静态图形看，这些并不复杂，然而一旦运动起来，尤其在旋转过程中，再去寻找数量关系，难度陡然上升，要么多种情况未考虑周全，要么直接就转晕了。而要解决好这些问题，则需要在草稿纸上多作图，如果平时这种功夫花得多，真到考场上，脑子里作图，角在心中动，那无疑最佳。

题目

已知点A，O，B在一条直线上，将射线OC绕O点顺时针方向旋转90°后，得到射线OD，在旋转过程中，射线OC始终在直线AB上方，且OE平分∠AOD.约定：无论∠AOD大小如何，OE都看作是由OA、OD两边形成的最小角的平分线.

(1)如图1，当∠AOC=30°时，∠BOD=_________；

(2)若射线OF平分∠BOC，求∠EOF的度数.

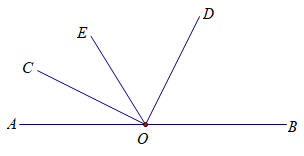
解析：

(1)给出特殊角度计算，初步了解题中角之间的联系，为后面动角打基础。∠AOC=30°，而且旋转角∠COD=90°，于是求得∠BOD=60°；

(2)本题难点在于射线OE的位置，而射线OE位置又取决于∠AOD，当我们在备用图中作图的时候，会发现，虽然题目限定了射线 OC始终在直线AB上方，可没有限制射线OD，毕竟经过顺时针旋转90°后，射线OD有可能到直线AB下方，那么麻烦就来了，通常我们在学习角平分线时，教材声明是小于180°的角.

①当射线OD在直线AB上方时，此时∠AOC为锐角，即∠AOC<90°，作图如下：

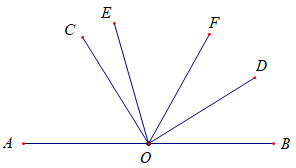
∠EOF到底和哪些角关联呢？似乎图中角都能和它产生联系，我们选择的原则是尽量与已知条件相近。因此选择∠EOF=∠DOE-∠DOF或∠EOF=180°-∠AOE-∠BOF，为了方便书写证明过程，不妨设∠AOC=x，推导如下：

②当OD与直线AB重合时，此时∠AOC=90°，显然∠AOD是一个平角，根据约定，它的角平分线OE与OC重合（注：为什么不是OC反向延长线？后文解释），如下图所示：

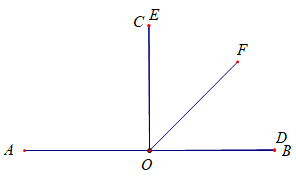
此时∠EOF=45°；

③当∠AOC>90°，即它是一个钝角时，情况又有不同，此时射线OD位于直线AB下方，如下图所示：

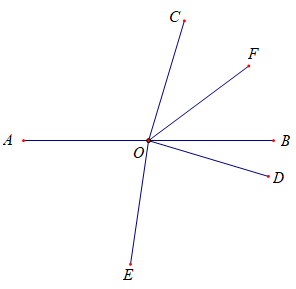
根据约定，OE是∠AOD的角平分线，它也在直线AB下方。此时∠EOF可看作三部分构成，即∠EOF=∠DOE+∠BOD+∠BOF，推导如下：

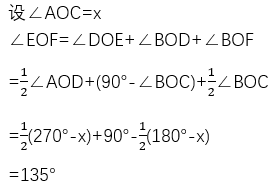
综上所述，∠EOF=45°或135°.

说明：关于角平分线定义，人教版七年级数学上册教材135页原文“一般地，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线。”，仅仅从这个定义描述出发，尚不足以说明当∠AOD为平角时，为何射线OE和OC重合，而不是它的反向延长线，于是我们又找到教材中关于角的定义，在第132页，原文“有公共端点的两射线组成的图形叫做角”，可对于题中的平角∠AOD而言，仍然有可能是指下方部分，直到同样这一页教材中，另外一段描述“角也可以看作是由一条射线绕着它的端点旋转而形成的图形。”

图中的∠AOD，就是这样形成的，因为题目描述中，规定的旋转方向为顺时针，即可以看作是射线OD从射线OA出发，顺时针旋转构成的图形，这也可以解释角的内部始终在直线AB上方，因此当射线 OD与射线OA变成平角的时候，它的角平分线OE和OC重合，而不是OC的反向延长线。

而一旦射线OD到直线AB下方，初中阶段未经特别说明，通常是指小于平角的角，因此∠AOD在直线AB下方，因此角平分线OE也在直线AB下方。

解题反思

本题理解上的主要困难在于对于动态角的把握，特别是旋转后超过平角时，角平分线位置发生了改变。同时这道题目也深度考察了学生对角的概念的理解，一般而言，角的定义我们通常用“有公共端点的两条射线组成的图形”，而很少用“一条射线绕着它的端点旋转而成的图形”，恰恰后者，就是从动态角度来解释角的概念。

七年级阶段，对于角的认知，除了度数关系之外，更多的是位置变化，在七年级下学期的平行线与相交线乃至八年级的全等三角形，无不对各种位置的角进行辨识、计算，因此，角的概念是否掌握牢固，非常重要。

微信公众号：爱数学做数学

相关内容