应力-应变曲线是开始研究材料时遇到的第一个材料强度图之一。

虽然它实际上并不难，但一开始可能看起来有点令人摸不着头脑。在本文中，我们将学习应力应变曲线的一些关键概念以便更好地理解它。

负载

使用中或制造过程中的金属会受到不同的力。根据这些力的大小，金属可能会或可能不会改变其形状。

施加力的行为称为负载。有五种不同的方式可以将这些力施加到金属部件上。

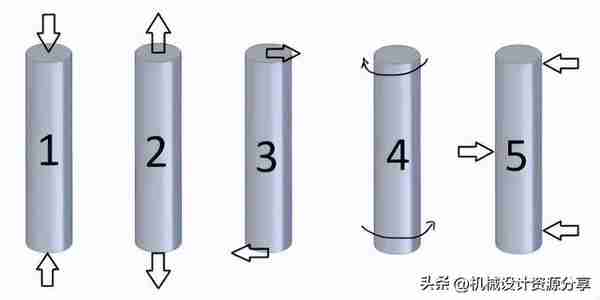
负载的五种形式是：

压缩

张紧

剪切

扭力

弯曲

金属在本质上具有一定的弹性。当承受载荷时，金属会发生变形，但如果没有特殊工具，它可能太小而无法识别。

当这个施加的力被移除时，金属会恢复其原始尺寸（除非力超过某个点）。例如，就像气球一样，在施加力后移除力后会恢复其原始形状。

什么是压力？

应力定义为所施加的力与其所施加到的材料的横截面积之比。

材料应力计算公式：

σ=F/A，其中

F 是力 (N)

A 是面积 (m 2 )

σ 是应力（N/m 2或 Pa）

例如，在 1 m 2的横截面积上施加 1 N 的力，将计算为 1 N/m 2 或 1 Pa的应力。单位可以同时显示为N/m2 或 Pa，两者均其中代表压力。

应力可以被理解为一个内部力在金属诱导响应于外部施加的力。它将尝试抵抗由外力引起的任何尺寸变化。

当横截面积发生变化时，相同的力会在金属中引起更大或更小的应力。较小的横截面积将导致较大的应力值，反之亦然。

什么是应变？

应变定义为尺寸变化与金属初始尺寸的比率。它没有单位。

存在三种类型的应变：法向、体积和剪切。

法向应变（或纵向应变）仅涉及一维的变化，例如长度。

应变计算公式为：

ε=(l*l 0 )/l 0，其中

l 0为起始或初始长度（mm）

l 为拉伸长度（mm）

例如，如果某个力将金属的长度从 100 毫米更改为 101 毫米，则法向应变将为 (101-100)/100 或 0.01。

根据外力的方向，法向应变可能为正或为负，因此会影响原始长度。

为简单起见，我们在文章中只讨论正常应变。因此，每次我们使用应变这个词时，它都会指代正常应变。一旦我们理解了正常应变，就很容易将同样的理解扩展到其他两个。

压力和应变

每当负载作用在物体上时，它就会在材料中产生应力和应变。

让我们以足球为例。当你试图挤压它时，它会产生阻力。提供的阻力是诱导应力，而尺寸变化代表应变。

应变导致应力。当施加导致变形的力时，材料试图通过设置内部应力来保持其主体结构。

如何绘制应力-应变曲线？

绘制应力应变曲线的最常用方法是对试件的一根杆进行拉伸试验。

这是使用万能试验机完成的。它有两个爪子，可以抓住杆的两个极端并以均匀的速度拉动它。

记录施加的力和产生的应变，直到发生断裂。然后将这两个参数绘制在 XY 图上以获得熟悉的图。

应力-应变曲线

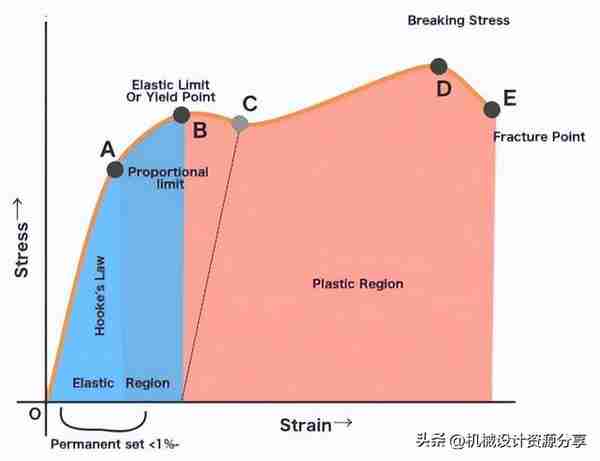
应力-应变曲线是显示应力随应变增加而变化的图表。它是材料科学和制造中广泛使用的金属参考图。

应力和应变曲线上有不同的部分，它们描述了延性材料根据引起的应力量而产生的不同行为。

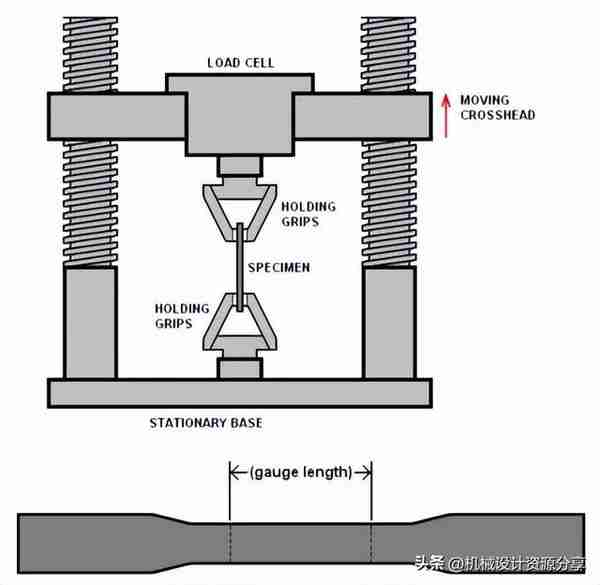
（拉伸试验图）

脆性、硬性（但非延展性）和塑性材料的应力和应变曲线是不同的。这些材料的曲线更简单，可以很容易地学习。我们将关注延性材料的应力-应变曲线。但在我们深入研究之前，让我们先看看另一个重要的概念——胡克定律。

胡克定律

这个物理学原理谈到了弹性，以及将弹性物体拉伸或压缩一定距离所需的力如何与该距离成正比。更多的力量产生更多的距离。

用于计算弹簧力的胡克定律公式：

就金属而言，胡克定律规定，对于大多数金属，长度变化越大，内力越大。这意味着应力与应变成正比。这是因为金属在一定限度内表现出弹性。

简单来说，如果拉伸/压缩载荷加倍，只要金属在比例限制内，长度的增加/减少也会加倍。

比例限制

几乎所有金属在特定范围内都表现得像弹性物体。该范围因不同的金属而异，并受机械性能、大气暴露（腐蚀）、晶粒尺寸、热处理和工作温度等因素的影响。

当试验机开始拉试件时，它会承受拉伸应力。最初，材料遵循胡克定律。

应变将与应力成正比。这意味着应力与应变的比率将是一个常数。在材料科学中，这个常数被称为杨氏弹性模量，是为应用选择合适材料时要考虑的最重要的机械特性之一。

没有永久变形。金属将像弹簧一样运行，并在移除负载时恢复到其原始尺寸。

观察到这种比例行为的点称为比例极限。随着应力的增加，应变线性增加。在上图中，此规则适用于收益率强度 指标。

杨氏弹性模量

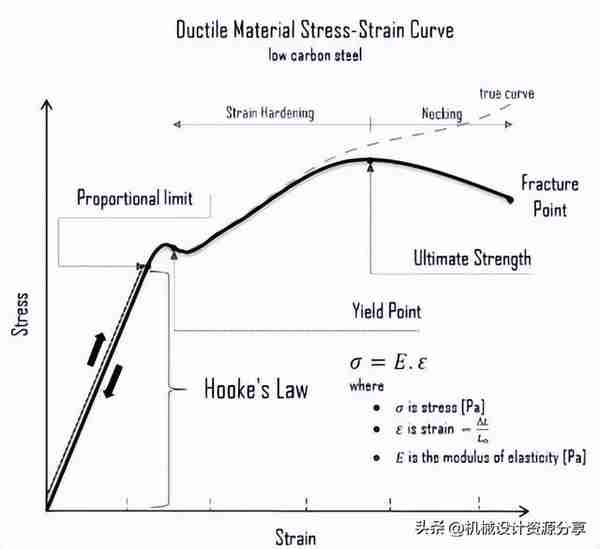
它被定义为材料的比例极限内的纵向应力与应变之比。也称为弹性模量，它类似于弹簧的刚度。这也是胡克定律包含弹簧常数的原因。

假设我们有 2 种具有相同长度和横截面的材料。为了以相同的方式改变尺寸，具有较高杨氏模量值的材料需要更大的力。

弹性点和屈服点

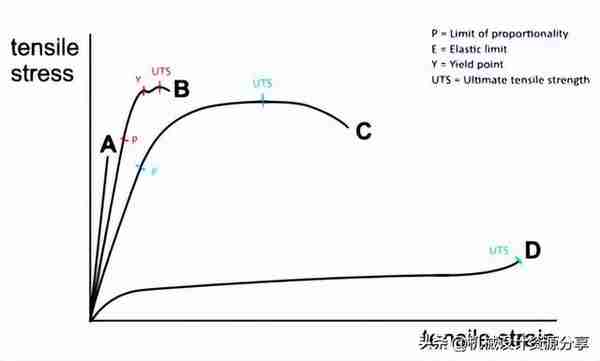
随着试样承受越来越大的拉力，应力会增加到超过比例极限。

应力-应变关系偏离胡克定律。应变以比应力更快的速度增加，这表现为应力和应变图中曲线的轻微变平。

这是图中第一条曲线开始但尚未向下转弯的部分。尽管应力与应变的比例消失了，但弹性的特性没有消失，并且在去除负载时，金属仍将恢复到其原始尺寸。

因此，弹性极限内的尺寸变化是暂时的和可逆的。材料的弹性极限决定了它在应力下的稳定性。

这就是工程计算使用材料的屈服强度来确定其抗负载能力的原因。如果载荷大于屈服强度，结果将是不需要的塑性变形。

塑性行为

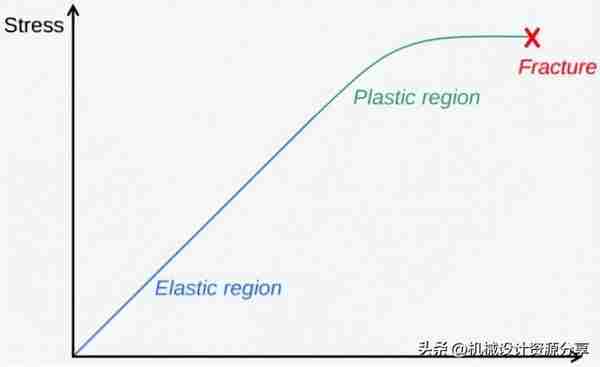
当试件在试验机上进一步拉动时，其弹性就丧失了。这与应力-应变图中应变硬化区域的开始一致。

屈服强度点是首先观察到材料塑性变形的地方。如果超过该点从试验机上松开材料，它将不会恢复到其原始长度。

当材料中的位错数量变得太高并且它们开始阻碍彼此的运动时，据说会发生应变硬化。材料不断地重新排列并趋于硬化。

颈缩

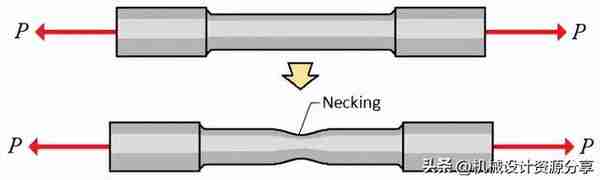
随着应力的增加，塑性变形继续发生。在适当的时候，将在杆上的一点处观察到横截面变窄。这种现象称为颈缩。应力如此之高，导致在杆的最薄弱点形成颈部。

应力应变曲线还显示了发生颈缩的区域。它的起点也为我们提供了材料的极限抗拉强度。

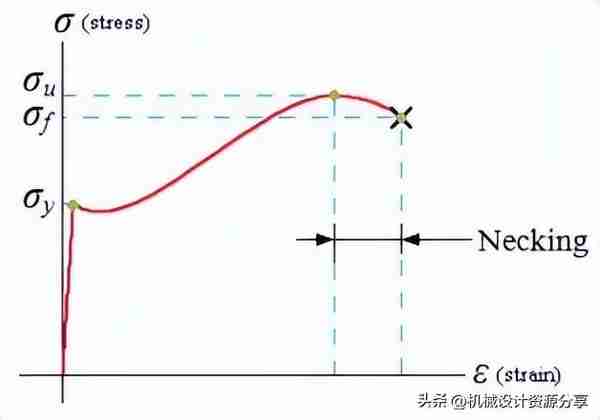
极限抗拉强度表示材料可以承受的最大应力。达到此值会将材料推向失效和断裂。

断裂

一旦进入颈缩区域，我们可以看到载荷不必增加以进行进一步的塑性变形。

颈部会发生断裂，通常在杆的两端形成杯形和锥形。该点称为断裂点或断裂点，在应力应变图上用 E 表示。

为什么应变-应力曲线很重要？

应力-应变曲线为设计工程师提供了一长串应用设计所需的重要参数。应力-应变图为我们提供了许多机械特性，例如强度、韧性、弹性、屈服点、应变能、回弹力和负载过程中的伸长率。

它还有助于制造。无论您是要执行挤压、轧制、弯曲还是其他一些操作，此图表中的值都将帮助您确定引起塑性变形所需的力。

相关内容